Discussing Scaling Laws for Neural Language Models (Paper review)

oluwatobi adefami / January 2023

Language modeling arguably accounts for a large part of the research carried out in the machine learning world, and the success deep learning has seen in this area of research has led to the creation of various SOTA models that have approached human-level performance on certain tasks. This paper studies emperical scaling laws for language model performance on the cross-entropy loss by investigating the the power-law relationship between loss and other variables including the model size, dataset size, and the magnitude of compute used for training a given transformer model.

Essentially, The paper demystifies the speculative expecation(s) involving dependence of model performance on factors like model architecture, neural model size, amount of compute available, and dataset size. Full paper is available here

The below figure shows the relationship observed between loss and increase in the scale of model size, dataset size and compute magnitude.

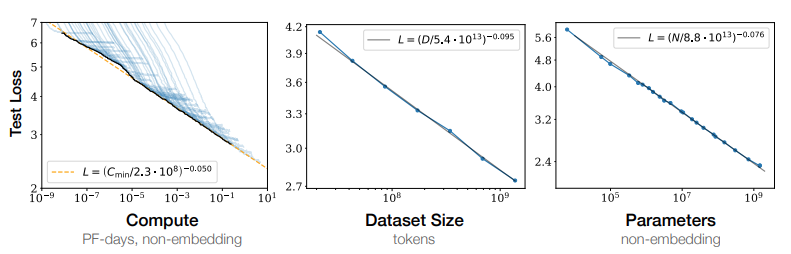Fig.1- Power-law scaling relationship between test loss and compute budget, dataset size, and model size respectively

[explanation: the power-law is a functional relationship between any two quantities; a relative change in one quantity causes a prportional relative change in the other quantity, independent of the initial magnitude of the quantities in question] –> provide more information on power-laws but do not make it exhausting

From the above diagram a few discussions could be drawn:

1. Model Performance depends more on scale than on shape: Scaling factors including the number of parameters N, the dataset size D, and the compute budget C used for training have been shown to play a more significant role in a model’s performance compared to other architectural hyperparameters such as depth vs width.

2. Smooth power-laws: The test loss L has a power law relationship with each of N, C, and D across several orders of magnitude (power law relationships are linear on a log-log scale).

3. Universatility of overfitting: The model’s performance improves predictably given that N and D are scaled in tandem, and a performance dips when N and D are held while other quantities are increased.

4. Universatility of training: Training curves follow predictable power-laws whose parameters are roughly independent of the model size.

5. Sample Efficiency: Large models reach the same level with fewer optimization steps while using fewer data points when compared to small models, making them more sample-efficient. this is shown in the figure below:

6. Convergence is inefficient: In an event where compute budget C is limited but there are no restrictions to the magnitude of the model size N and dataset size D, optimal performance is attained by training very large models and stopping short of convergence.

7. Optimal batch size: It was discovered that the batch size required to train the models is roughly a power of the loss only, and continues to be determined by measuring the gradient of the noise scale [MKAT18];

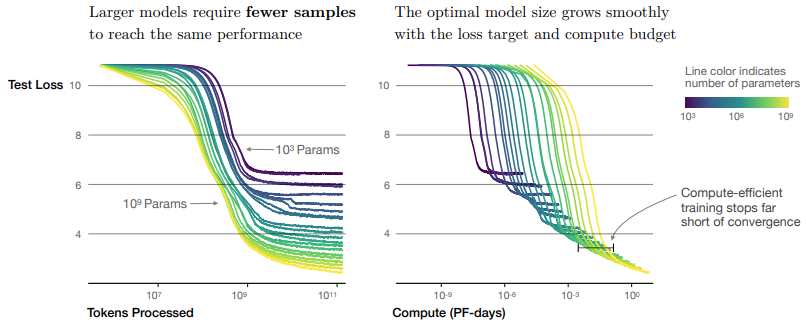Fig.2- large models are more sample efficient